python代码写了两种,一个是机器学习实战的纯python,一个是sklearn包。
1、决策树通俗理解
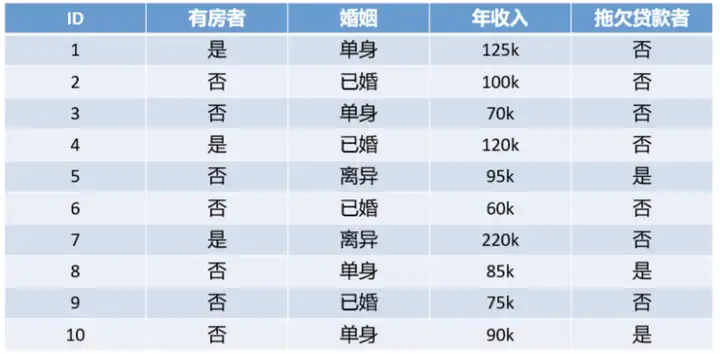
首先用一个简单的例子来认识决策树是什么,这有一份数据,问题是判断是否会拖欠贷款,其中有房者、婚姻和年收入是三个特征(或者属性),拖欠贷款者是分类的标签。
示例数据表
然后我们来构建一颗决策树。
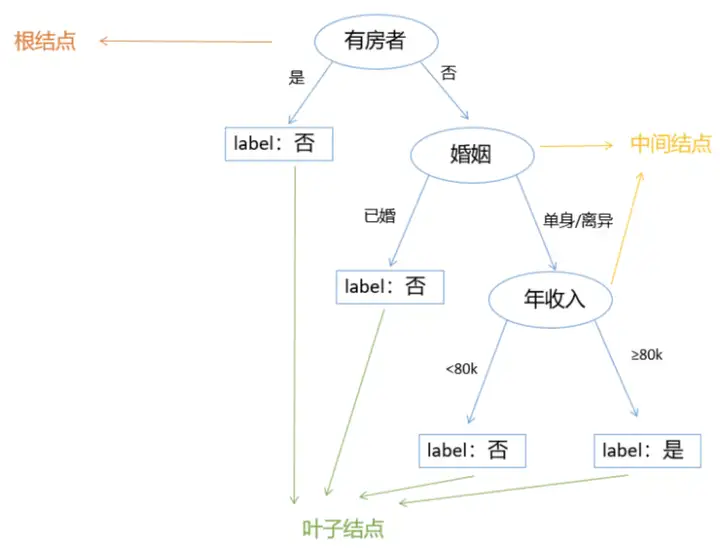
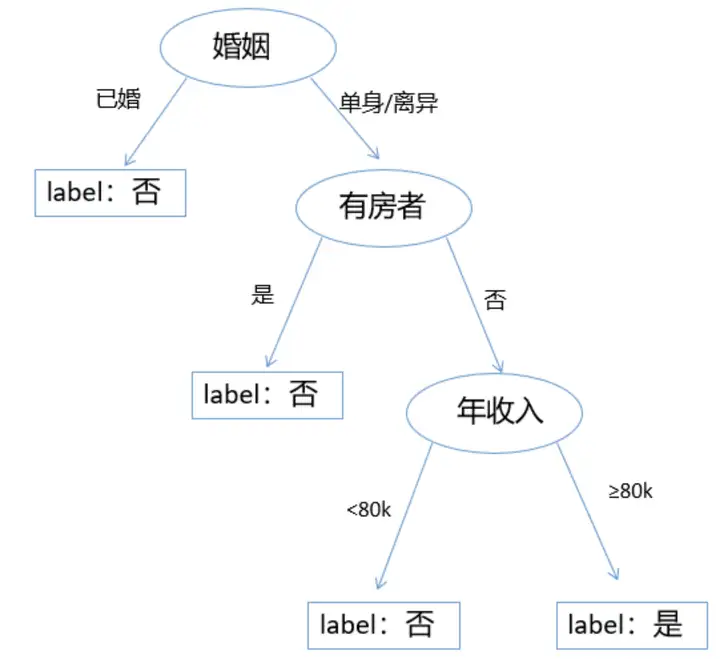
构建决策树示例图
第一个特征包含是和否两类,其中为是的均不是拖欠贷款者,可以把label设为否,其中为否的需要进一步划分。第二个特征婚姻包含已婚、单身和离异三种,我们可以分为两大类,其中已婚的均不是拖欠贷款者,label设为否,单身和离异的需要进一步划分。第三个特征年收入,我们可以分为小于80k和大于80k,最终得到label的标签,这样就构建出了一颗决策树,如图4所示。其中有房者是根结点,无入边有出边;婚姻和年收入是中间结点,有入边也有出边,方形的这几个是叶子结点,有入边无出边。
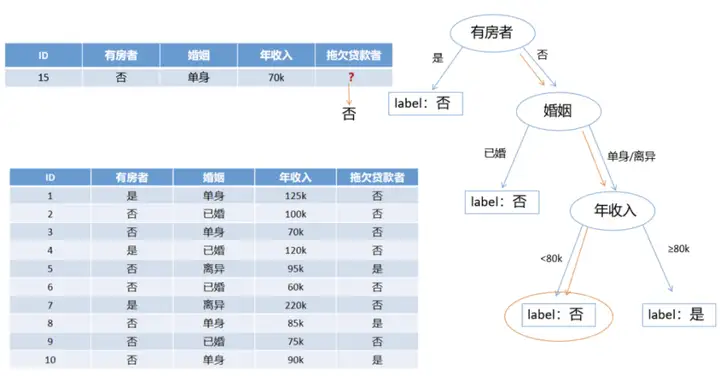
构建出决策树后如何使用呢?比如来了一条新的数据,我们就可以通过特征判断,最后得到是否标签,也就是预测结果是否。
决策树预测示例
了解了决策树是什么以及怎么用之后,决策树算法就是解决如何构建决策树的问题。主要分为三大部分,先从整体讲一下三部分是什么。
第一部分,决策树的特征选择。因为决策树本身是个分类做决策的过程,那么对我们做决策有影响的那些事物,就是决策树的特征。在决策树算法当中的专业术语,就是叫信息增益或者信息增益比或者基尼指数,来对特征进行选择。
第二部分,决策树的生成。求完特征之后,就是如何去生成一颗庞大的决策树,其实就是,哪一个特征是树的根节点,哪个特征是树的中间节点,这个就是我们去计算特征值之后,再利用这个决策树的算法去构造这样一颗树。信息增益对应的决策树的算法是ID3这个算法,信息增益比对应的就是c4.5这个算法,基尼指数是CART算法,就是用这样的一个算法去构造一颗决策树。
第三部分,决策树的剪枝。因为一棵树,如果说只针对这一个训练集,来生成一棵树,那可能是这棵树只适合这个训练集,那么这时可能会出现过拟合的状态,因为他只适合这个训练集,不能适合所有的数据样本,所以说我们要把那种非常极端的说白了就是只适合这个训练集的那些枝枝叶叶给它剪掉,这个就是决策树的剪枝,目的就是防止过拟合,让决策树泛化能力更强。
(1) 决策树的特征选择
分了两个小点,第一个是如何通过特征构建结点,还是以这个数据为例,有房者是二元属性,可以按照是和否分为两类;婚姻是多元属性,我们可以分为多元的三类也可以分为两个大类;年收入是叙述属性,我们通过分组来划分,比如分为两类或三类。第二点就是特征选择,这里用到了两个熵和基尼这两个指标。
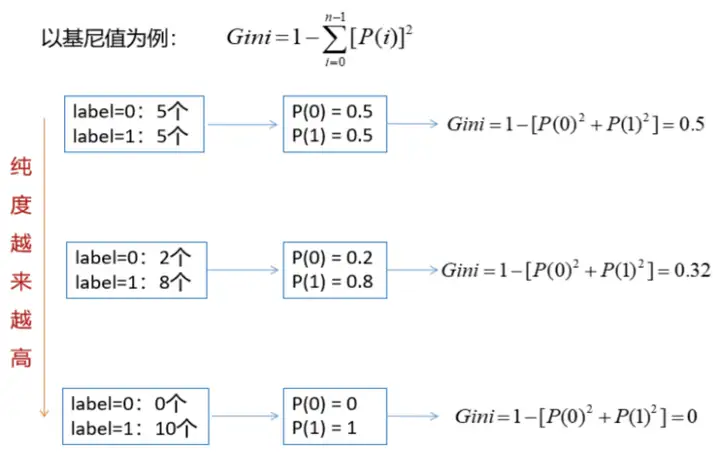
基尼值含义介绍
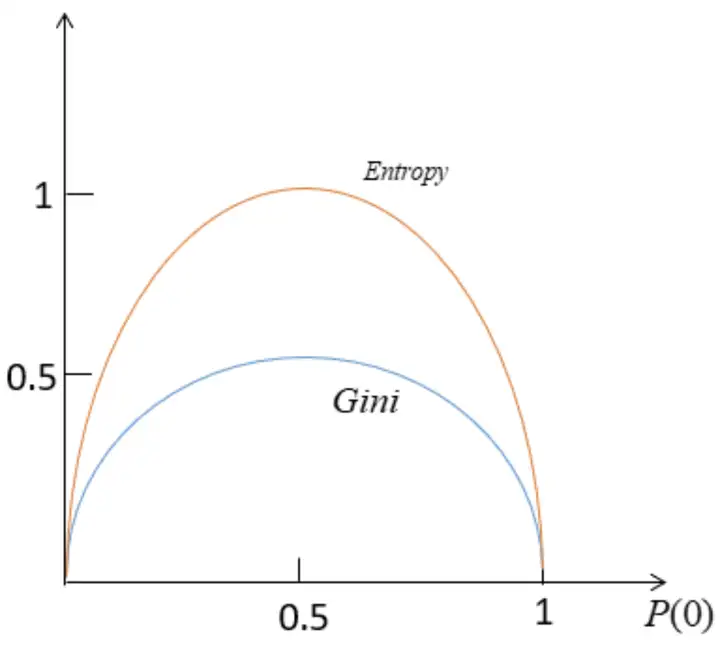
以基尼为例简单介绍一下,式中的P(i)是指标签为i的概率,上面给了三组:第一组标签为0和标签为1的个数都是五个,得到他们的概率都是0.5,计算出基尼值为0.5;第二组标签为0的有两个,标签为1的有8个,最终计算出基尼值为0.34;第三组全部为1标签,计算出基尼值为0。可以看出,从上到下,纯度是越来越高的,伴随着基尼值越来越小。我们可以得到基尼值的曲线,在0.5的时候纯度最低。同理,我们也可以得到熵是这样的。
熵值曲线与基尼值曲线图
当我们对特征进行选择时,我们就是计算基于熵或者基尼的信息增益、信息增益比、基尼指数来进行划分。比如信息增益的计算方法,分别计算出经验熵和经验条件熵后求差。
信息增益计算方法
因为信息增益会偏向类别比较多的特征,所以又提出信息增益比。
(2) 决策树的生成
以ID3算法为例介绍一下,输入就是训练数据集D、特征集A、阈值。阈值其实在机器学习算法中都会涉及到阈值,因为在无限迭代下去的时候,可能近两次迭代的值是非常接近的,这时候就没必要再迭代下去了,那么我们就需要设置一个阈值,让阈值来控制迭代停止。就是这个时候模型已经稳定的可以得到结果了。输出就是决策树T。
ID3算法步骤
这里写了六个步骤,其中几条都是特殊情况。核心步骤就是第三步,计算A中各特征对D的信息增益,选择信息增益最大的特征,然后返回子树,递归调用。C4.5算法、CART算法也是类似,只不过换成信息增益比或基尼指数,然后基尼指数的话,是选择基尼指数最小的。
然后以前面提到的数据为例,使用CART算法构建出的决策树如图10所示。
CART算法构建的决策树
开始计算出婚姻的基尼指数是最小的,然后在剩下两个中,有房者的基尼指数更小,最终构建完成。
(3) 决策树的剪枝
决策树剪枝的方法就是极小化决策树整体的损失函数。决策树只考虑了通过提高信息增益(或信息增益比)对训练数据进行更好的拟合。而决策树的剪枝通过优化损失函数还考虑了减小模型复杂度。决策树生成学习局部的模型,而决策树剪枝学习整体的模型。
2、决策树理论整理
ID3算法
C4.5算法
3、决策树代码
(1)机器学习实战中纯python
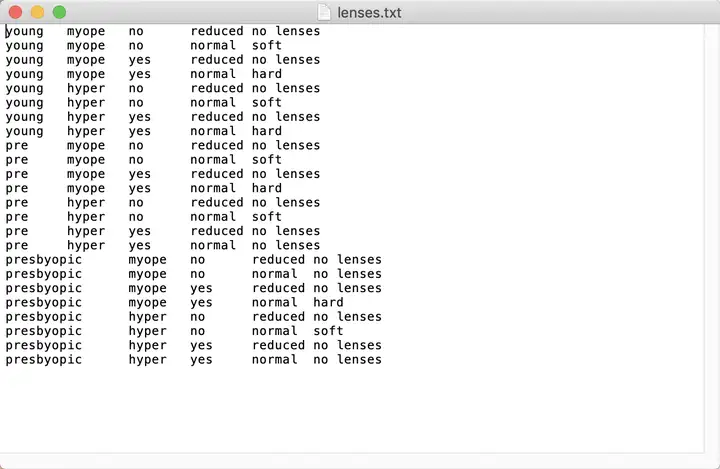
在最下面做了两个数据集测试,下图是第二个测试的数据。
测试2数据集
from math import log
import operator
import matplotlib.pyplot as plt
import pickle
#计算熵:度量数据集的无序程度
def calcShannonEnt(dataSet): #dataSet包括特征和label,最后一列为label
numEntries = len(dataSet)
labelCounts = {}
#统计各标签值的数量
for featVec in dataSet:
currentLabel = featVec[–1] #取最后一列:label标签值
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
#计算熵:-sum(pi*logpi),每个特征值的熵求和
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries #计算每个特征的概率值
shannonEnt -= prob * log(prob,2) #计算每个特征的熵值
return shannonEnt
#划分数据集:将符合要求的元素抽取出来
def splitDataSet(dataSet, axis, value):
dataSet:待划分的数据集
axis:选定的特征名称
value:需要返回的特征的值
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #chop out axis used for splitting
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
#选择出能划分数据集的最好的特征
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) – 1 #特征数(最后一列是特征值,所以减一)
baseEntropy = calcShannonEnt(dataSet) #计算数据集的当前整体熵
bestInfoGain = 0.0
bestFeature = –1
#遍历所有特征,计算用该特征分类后的信息增益,选择出最大的信息增益的特征作为最优特征
for i in range(numFeatures):
featList = [example[i] for example in dataSet] #提取该特征列所有数据
uniqueVals = set(featList) #set()函数创建一个无序不重复元素集,即特征都包含哪些特征值(比如是否有房这个特征,就包含是和否两个元素)
#计算当前特征分类的信息熵
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy – newEntropy #计算信息增益:整体熵-当前特征信息熵
#选择最大的信息增益
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature #返回特征索引值
#计算出现次数最多的类别
def majorityCnt(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
#创建树
def createTree(dataSet,labels):
dataSet:数据集,包括特征和标签
labels:标签列表,算法本身是不需要这个参数的,这里是为了给出数据明确的含义
classList = [example[–1] for example in dataSet] #取最后的标签label列
#停止条件1:类别完全相同则停止划分
if classList.count(classList[0]) == len(classList):
return classList[0]
#停止条件2:已遍历完所有特征,返回出现次数最多的类别
if len(dataSet[0]) == 1:
return majorityCnt(classList)
#选择最好的特征
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}} #将选择出的特征添加进树(myTree包含了代表树结构信息的嵌套字典)
labels2 = labels.copy()
del(labels2[bestFeat]) #在labels中删除已经选择过的特征
featValues = [example[bestFeat] for example in dataSet] #取出选择特征的所有特征值
uniqueVals = set(featValues) #取出选择特征都包含哪些元素
for value in uniqueVals:
subLabels = labels2[:] #复制所有标签,这样树就不会弄乱现有的标签
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
#使用决策树进行分类
def classify(inputTree,featLabels,testVec):
inputTree:构建好的决策树
featLabels:特征列表
testVec:待分类的测试数据
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr) #取第一个特征在特征列表中的索引
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat, dict):
classLabel = classify(valueOfFeat, featLabels, testVec)
else: classLabel = valueOfFeat
return classLabel
#存储决策树
def storeTree(inputTree,filename):
fw = open(filename,w)
pickle.dump(inputTree,fw)
fw.close()
#读取决策树
def grabTree(filename):
fr = open(filename)
return pickle.load(fr)
##############下面是绘制树形图的###########
#定义文本框和箭头格式
decisionNode = dict(boxstyle=“sawtooth”, fc=“0.8”)
leafNode = dict(boxstyle=“round4”, fc=“0.8”)
arrow_args = dict(arrowstyle=“<-“)
#获取叶节点的数目
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__==dict: #测试节点的数据类型是都为字典,如果不是,则为叶节点
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
#获取树的层数
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__==dict: #测试节点的数据类型是都为字典,如果不是,则为叶节点
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
#绘制带箭头的注解
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords=axes fraction,
xytext=centerPt, textcoords=axes fraction,
va=“center”, ha=“center”, bbox=nodeType, arrowprops=arrow_args )
#在父子文本间填充文本信息
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]–cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]–cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va=“center”, ha=“center”, rotation=30)
#绘制树
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
myTree:
parentPt:
nodeTxt:
#计算宽与高
numLeafs = getNumLeafs(myTree) #决定树的宽度
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0] #此节点的文本标签
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
#标记子节点属性值
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff – 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__==dict: #测试节点的数据类型是都为字典,如果不是,则为叶节点
plotTree(secondDict[key],cntrPt,str(key)) #递归
else: #its a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#绘制主函数
def createPlot(inTree):
fig = plt.figure(1, facecolor=white)
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = –0.5/plotTree.totalW; plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), )
plt.show()
############### 测试1 ###############
dataSet = [[1, 1, yes],
[1, 1, yes],
[1, 0, no],
[0, 1, no],
[0, 1, no]]
labels = [no surfacing,flippers]
#创建树
myTree = createTree(dataSet,labels)
print(“构造的决策树为:”, myTree)
#分类测试
test_result1 = classify(myTree, labels, [1,0])
print(“特征[1,0]所属类别为:”, test_result1)
test_result2 = classify(myTree, labels, [1,1])
print(“特征[1,1]所属类别为:”, test_result2)
#绘制树形图
createPlot(myTree)
############### 测试2 ###############
fr = open(lenses.txt)
lenses = [inst.strip().split(\t) for inst in fr.readlines()]
lensesLabels = [age, precript, astigmatic, tearRate]
#创建树
lensesTree = createTree(lenses, lensesLabels)
print(“构造的决策树为:”, lensesTree)
#分类测试
test_result1 = classify(lensesTree, lensesLabels, [pre, hyper, no, normal])
print(“特征[pre, hyper, no, normal]所属类别为:”, test_result1)
test_result2 = classify(lensesTree, lensesLabels, [young, hyper, yes, reduced])
print(“特征[young, hyper, yes, reduced]所属类别为:”, test_result2)
#绘制树形图
createPlot(lensesTree)
运行结果:
(2)sklearn
数据:
代码:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
from sklearn.metrics import accuracy_score,classification_report, confusion_matrix
# from utilities import visualize_classifier
from io import StringIO
import pydotplus
from sklearn.tree import export_graphviz
import pylab as pl
pd.set_option(precision,4)
dataset = pd.read_csv(“dtree_data.csv”, header=None,names=[0,1,2])
print(dataset.head())
print(dataset.tail())
X = dataset.iloc[:, :–1]
y = dataset.iloc[:, –1]
# 划分训练集、测试集
X_train, X_test, y_train, y_test =train_test_split(X, y, test_size=0.20, random_state=5)
# 创建分类器
clf = DecisionTreeClassifier(criterion=gini, random_state=0)
# 训练模型
clf.fit(X_train, y_train)
# 预测
y_pred = clf.predict(X_test)
# 评价模型
accuracy = np.round(accuracy_score(y_test, y_pred),3)
print(“Accuracy of the new classifier =”, accuracy)
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
# decision boundary
plt.figure()
X=np.array(X_test)
y=np.array(y_pred)
x_min, x_max = X[:,0].min() – 0.1, X[:,0].max() + 0.1
y_min, y_max = X[:,1].min() – 0.1, X[:,1].max() + 0.1
h = 0.02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
pl.set_cmap(pl.cm.Paired)
pl.pcolormesh(xx, yy, Z)
# Plot the training points
for i in range(len(X)):
if y[i] == 0:
_ = pl.scatter(X[i,0], X[i,1], c=red, marker=o)
elif y[i] == 1:
_ = pl.scatter(X[i,0], X[i,1], c=blue, marker=x)
elif y[i] == 2:
_ = pl.scatter(X[i,0], X[i,1], c=green, marker=+)
else:
_ = pl.scatter(X[i,0], X[i,1], c=magenta, marker=v)
pl.xlabel(Petal length)
pl.ylabel(Petal width)
pl.xlim(x_min,x_max)
pl.ylim(y_min, y_max)
pl.show()
运行结果: